Introduction
Start with a brief introduction to Kruskal’s algorithm, explaining its purpose and how it fits into the broader context of graph theory and minimum spanning trees (MST).
Input
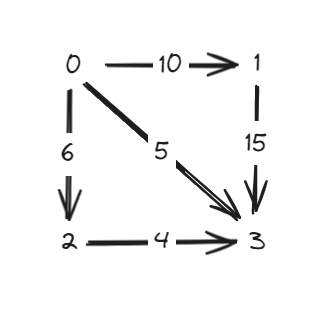
Output
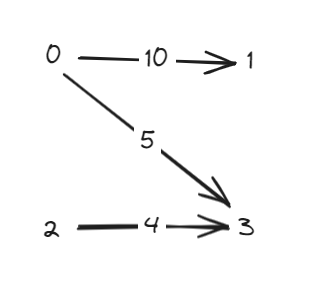
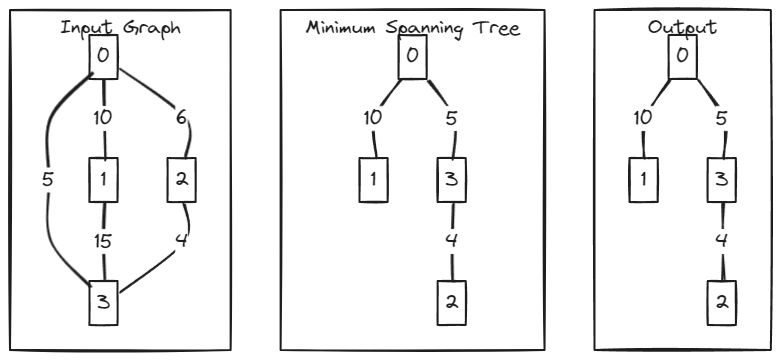
Java Code Explanation
Edge Class
Explain the Edge class:
class Edge implements Comparable<Edge> {
int source, destination, weight;
public Edge(int source, int destination, int weight) {
this.source = source;
this.destination = destination;
this.weight = weight;
}
@Override
public int compareTo(Edge other) {
return this.weight - other.weight;
}
}- Describe how the
Edgeclass represents an edge with source, destination, and weight. - Highlight the
compareTomethod used for sorting edges by weight.
UnionFind Class
Explain the UnionFind class:
class UnionFind {
private final int[] parent;
private final int[] rank;
public UnionFind(int size) {
parent = new int[size];
rank = new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
rank[i] = 0;
}
}
public int find(int u) {
if (u != parent[u]) {
parent[u] = find(parent[u]);
}
return parent[u];
}
public void union(int u, int v) {
int rootU = find(u);
int rootV = find(v);
if (rootU != rootV) {
if (rank[rootU] > rank[rootV]) {
parent[rootV] = rootU;
} else if (rank[rootU] < rank[rootV]) {
parent[rootU] = rootV;
} else {
parent[rootV] = rootU;
rank[rootU]++;
}
}
}
}- Describe the
UnionFindclass used for union-find operations, which are crucial for cycle detection.
KruskalAlgorithm Class
Explain the main KruskalAlgorithm class:
public class KruskalAlgorithm {
private final int vertices;
private final Edge[] edges;
public KruskalAlgorithm(int vertices, Edge[] edges) {
this.vertices = vertices;
this.edges = edges;
}
public void kruskalMST() {
Arrays.sort(edges);
UnionFind uf = new UnionFind(vertices);
Edge[] result = new Edge[vertices - 1];
int edgeIndex = 0;
for (Edge edge : edges) {
if (edgeIndex == vertices - 1) break;
int sourceRoot = uf.find(edge.source);
int destinationRoot = uf.find(edge.destination);
if (sourceRoot != destinationRoot) {
result[edgeIndex++] = edge;
uf.union(sourceRoot, destinationRoot);
}
}
System.out.println("Edges in the Minimum Spanning Tree:");
for (Edge edge : result) {
System.out.println(edge.source + " - " + edge.destination + ": " + edge.weight);
}
}
public static void main(String[] args) {
int vertices = 4; // Number of vertices in the graph
Edge[] edges = {
new Edge(0, 1, 10),
new Edge(0, 2, 6),
new Edge(0, 3, 5),
new Edge(1, 3, 15),
new Edge(2, 3, 4)
};
KruskalAlgorithm kruskal = new KruskalAlgorithm(vertices, edges);
kruskal.kruskalMST();
}
}- Explain how the
KruskalAlgorithmclass initializes and executes Kruskal’s algorithm to find the Minimum Spanning Tree (MST). - Describe the
kruskalMSTmethod, which sorts edges, applies union-find to detect cycles, and prints the MST edges.
Conclusion
Summarize Kruskal’s algorithm and its significance, possibly mentioning its applications and complexity.